Um joão-bobo da loja de fruta.
Se você cortar algumas laranjas perceberá que,…
…independente da altura…
…todos os pedaços se detêm…
…com a face cortada na posição horizontal.
Exceto em um declive.
www.ciesacao.org | Os experimentos mão na massa da Ciênsação são publicados como Recursos Educacionais Abertos sob a licença Creative Commons Attribution-ShareAlike 4.0 International License.
Um joão-bobo da loja de fruta.
Se você cortar algumas laranjas perceberá que,…
…independente da altura…
…todos os pedaços se detêm…
…com a face cortada na posição horizontal.
Exceto em um declive.
Dança das frutas
É muito comum ver um pedaço de maçã ou de laranja balançando sobre uma mesa. Essa situação do dia a dia nos oferece uma boa oportunidade para introduzir ou reforçar conceitos importantes da Mecânica como momento angular, centro de massa e equilíbrio.
Embora a tarefa possa parecer bem simples, a física e a matemática envolvidas são complexas: enquanto uma discussão qualitativa pode ser feita em poucos minutos, uma rigororsa análise quantitativa pode facilmente entreter um físico por um dia inteiro.
Treinar encontrar o centro de massa, eixos de rotação e momento angular em um sistema mecânico.
Analisar a mecânica de brinquedos do tipo joão-bobo (ou sempre-em-pé).
Faca
Cortar algumas laranjas em duas partes (não cortar todas as frutas ao meio) e dar um pedaço para cada grupo.
Coloque o pedaço de laranja em uma superfície horizontal.
1. Por que a fruta balança e sempre se detêm com a face cortada na posição horizontal?
2. O que acontece em um declive?
(se for necessário)
Quando está sobre a superfície, a fruta roda em torno de qual eixo?
› Em torno do centro geométrico da esfera, ou seja, em volta da fruta inteira, mesmo que este centro tenha sido cortado.
Onde está o centro de massa de cada pedaço?
› Em uma fruta inteira, o centro de massa está no centro geométrico; nos pedaços de fruta, o centro de massa está abaixo do centro geométrico.
O que acontece se você inclinar a fruta?
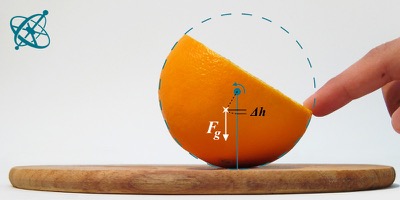
› Você levanta o centro de massa (ver imagem).
Por que a fruta se inclina para um lado em um declive?
› Porque essa é a posição com a menor energia potencial. Inclinando a fruta mais – ou menos – eleva-se o centro de massa.
Se cortarmos a parte superior da esfera, em qualquer altura, o centro de massa da parte restante estará abaixo do centro geométrico da esfera. Inclinando a fruta, por conseguinte, aumenta-se o centro de massa. Assim como um joão-bobo, o fruto vai balançar ou oscilar por algum tempo antes de deter-se em equilíbrio com a energia potencial mínima: com a face cortada na posição horizontal. Numa superfície não horizontal (com atrito suficiente para evitar o deslizamento), o movimento angular em torno do centro da esfera é contrariado por um outro momento angular que o centro de massa gera em torno do ponto de apoio (onde a laranja toca a superfície). Sob essas condições, o fruto irá se equilibrar com a face de corte inclinada, e o ângulo entre a superfície e parte cortada depende da altura de corte e da inclinação.