Ouça o chamado da gravidade da Terra.
Amarre pesos num barbante e a distâncias iguais.
Uma opção rápida é…
…usar clipes de papel e porcas.
Em seguida, segure o barbante e ouça a queda.
www.ciesacao.org | Os experimentos mão na massa da Ciênsação são publicados como Recursos Educacionais Abertos sob a licença Creative Commons Attribution-ShareAlike 4.0 International License.
Ouça o chamado da gravidade da Terra.
Amarre pesos num barbante e a distâncias iguais.
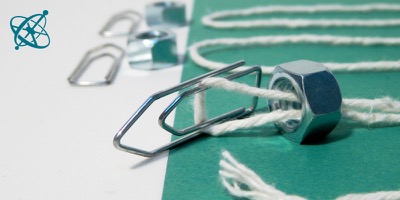
Uma opção rápida é…
…usar clipes de papel e porcas.
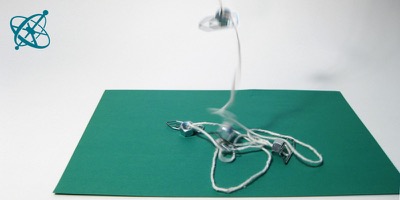
Em seguida, segure o barbante e ouça a queda.
Queda livre
A força gravitacional, que Newton compreendeu por causa de maçãs que caíram sobre ele, acelera tudo em direção ao centro da Terra. Com essa experiência, os alunos podem ouvir esta aceleração g como uma batida crescente. E, se consiguirem modificar a configuração para que a aceleracão gere uma batida constante, eles poderão demonstrar que entendem as leis subjacentes da física.
Ouvir a aceleração gravitacional.
Transformar modelos matemáticos em soluções práticas.
Pesos que possam ser facilmente amarrados ao barbante
Régua
Preparar para cada grupo um barbante de 2m de comprimento e 6 pesos que possam ser facilmente amarrados a ele. As porcas e clipes vistos nas fotos são apenas uma sugestão.
Ouça o som dos pesos caindo.
1. Por que é a batida vai aumentando?
2. A qual distância você precisa prender os pesos a fim de obter uma batida constante?
(se for necessário)
No momento em que você soltar o barbante, qual é a velocidade de queda dos pesos?
› Nenhuma.
O primeiro e o último peso batem no chão na mesma velocidade?
› Não, o último acelera durante mais tempo e, por conseguinte, atinge o solo a uma velocidade maior.
Quão longe cai um objeto em um tempo determinado?
› A partir das leis de Newton podemos deduzir que h = 0.5 g t2.
Se você quiser que o tempo t entre dois pesos que batem no chão seja o mesmo, a que distância h os pesos devem estar separados?
› As distâncias aumentam com o número de cada peso elevado ao quadrado: h1 = k 12, h2 = k 22,..hn = k n2, onde k pode ser qualquer constante, por exemplo, k = 5 cm..
Os pesos aceleram enquanto caem. Cada peso, por conseguinte, atinge o solo a uma velocidade mais elevada do que o anterior, exigindo menos tempo para cobrir a distância entre dois pesos. Assim, o tempo entre dois pesos para atingir o solo torna-se mais curto e um observador ouve um aumento da batida.
Para gerar uma batida constante, o que deve ser constante não é a distância entre os pesos, mas o tempo que demoram os dois pesos para bater no chão. Como h ~ t2, a distância tem que aumentar com o número do peso elevado ao quadrado n, ou seja, hn~ n2. Uma solução possível é fixar os pesos a distâncias de 5 cm, 20 cm, 45 cm, 80 cm, 125 cm e 180 cm.